课堂规模悖论

在《Think Stats 2nd》书中的第三章提到了一个有趣的统计学悖论——课堂规模悖论。书中表述如下：

在很多美国大学和学院里，学生与教师的比例约为10：1，但是学生们经常会惊讶地发现自己课上的平均学生数大于10，造成这一现象的原因有两个：

学生通常每学期修4到5门课，但是教授经常只教1门或2门；
上小课的学生很少，但上大课的学生人数非常之多。

一旦我们知道了第一个原因，其效应就是显而易见的，第二个就不那么明显了。让我们来看一个例子，假设一所学院某学期开了65门课，选课的人数分布如下：

size	count
5-9	8
10-14	8
15-19	14
20-24	4
25-29	6
30-34	12
35-39	8
40-44	3
45-49	2

如果你问院长，每门课平均的选课人数是多少，他会构建一个PMF( probability mass function，概率质量函数），计算出均值。

PMF是将数据中的每个值映射到其概率上，是除直方图外的另一种表示数据分布的方法。

书中的代码使用的是作者自建的一个python库thinkstats2，这里不再赘述，只是借书中的例子，用python还原如下：

#定义选课人数分布字典
d = {7:8,12:8,17:14,22:4,27:6,32:12,37:8,42:3,47:2}
#获取人数分布的array
data = numpy.array(list(d.keys())).repeat(list(d.values()))
#计算均值
act_mean = data.mean()

计算得到实际选课人数均值约为23.7。

这是我们获取全部数据之后，站在类似于上帝视角去看的结果，那么如果我们对一组学生进行调查，询问他们的课堂上有多少学生，然后再次计算均值，会发现什么呢？

首先，计算出学生观察到的分布，其中每个课堂规模值的概率受到选课学生人数的“影响”。

具体实现：假设每门课的选课人数为x，而该规模人数的课程出现的概率为p，那么通过询问，获得的该规模课程总数应该为x*p。

#我们先构建课程规模与课程出现概率的字典
pmf = {size:(count/65) for size,count in d.items()}#65为课程总数

#构建课程规模与询问后得到的课程计数字典，我们把它叫做偏倚分布
obs_data = {size:size*count for size,count in pmf.items()}
#计算偏倚分布的选课人数总数
sum_students = sum(list(map(lambda x:x[0]*x[1],zip(obs_data.keys(),obs_data.values()))))
#计算偏倚分布的总课程数
sum_count = sum(list(obs_data.values()))
#计算偏倚分布的选课人数均值
obs_mean = sum_students/sum_count

计算得到的结果为：29.1，比实际的均值高了约25%。

接下来，我们构建这两组数据的PMF图，能更直观一些。

#构建偏倚分布课程规模与该课程出现概率的字典
obs_pmf = {size:count/sum_count for size,count in obs_data.items()}

#可视化，并列柱状图
sns.set(style="white", context="talk")#设置样式

fig = plt.figure(figsize = (10,5))#设置图像大小
ind = np.array(list(pmf.keys()))
width = 0.4

plt.bar(ind - width,pmf.values(),label = 'actual')#实际值

plt.bar(ind + width,ano_pmf.values(),label = 'observed')#观察值

plt.xlabel('class size')
plt.ylabel('PMF')
plt.xticks(list(pmf.keys()))
plt.legend(loc='upper right');

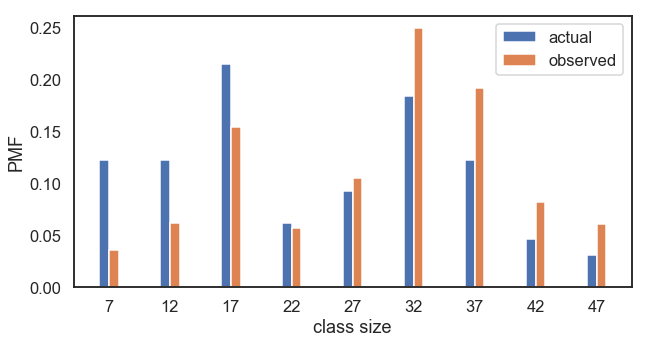
从图中可以明显看出，在偏倚分布中，小课更少，大课更多。

同样，你也可以反向进行如上的操作。假设你希望得到一所学院的课堂规模分布，但却无法从院长处得到可靠数据，你可以采用另一个办法：选择学生的一个随机样本，进行调查，询问他们的课堂上有多少学生，然后再进行“去偏倚”的操作，这里就需要用统计得来的同等规模课程计数除以它出现的概率。